문제
2613번: 숫자구슬
첫째 줄에 구슬의 개수 N과 그룹의 수 M이 주어진다. 둘째 줄에는 각 구슬이 적혀진 숫자가 왼쪽부터 차례로 주어진다. N은 300 이하의 자연수, M은 N이하의 자연수이며, 구슬에 적혀진 숫자는 100
www.acmicpc.net
문제이해
N개의 숫자 구슬이 <그림 1>과 같이 막대에 꿰어져 일자로 놓여 있다. 이들 구슬은 막대에서 빼낼 수 없고, 바꿀 수 없다.
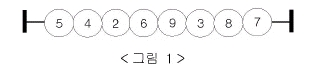
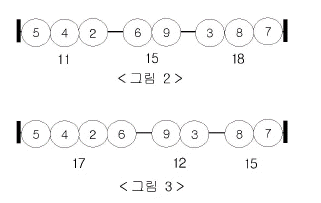
이 숫자 구슬을 M개의 그룹으로 나누었을 때 각각의 그룹의 합 중 최댓값이 최소가 되도록 하려 하다. 예를 들어 세 그룹으로 나눈다고 할 때 <그림 2>와 같이 그룹을 나누면 그룹의 합은 각각 11, 15, 18이 되어 그 중 최댓값은 18이 되고, <그림 3>과 같이 나누면 각 그룹의 합은 각각 17, 12, 15가 되어 그 중 최댓값은 17이 된다. 숫자 구슬의 배열이 위와 같을 때는 그룹의 합 중 최댓값이 17보다 작게 만들 수는 없다. 그룹에 포함된 숫자 구슬의 개수는 0보다 커야 한다.
각 그룹의 합 중 최댓값이 최소가 되도록 M개의 그룹으로 나누었을 때, 그 최댓값과 각 그룹을 구성하는 구슬의 개수를 찾아 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 구슬의 개수 N과 그룹의 수 M이 주어진다. 둘째 줄에는 각 구슬이 적혀진 숫자가 왼쪽부터 차례로 주어진다. N은 300 이하의 자연수, M은 N이하의 자연수이며, 구슬에 적혀진 숫자는 100 이하의 자연수이다.
출력
각 그룹의 합 중 최댓값이 최소가 되도록 M개의 그룹으로 나누었을 때 그 최댓값을 첫째 줄에 출력하고, 둘째 줄에는 각 그룹을 구성하는 구슬의 개수를 왼쪽부터 순서대로 출력한다. 구슬의 개수를 출력할 때는 사이에 한 칸의 공백을 둔다. 만약 그룹의 합의 최댓값이 최소가 되도록 하는 경우가 둘 이상이라면 그 중 하나만을 출력한다.
풀이
문제를 처음 접했을 때 떠오르는 알고리즘이 없어 다른 분들의 풀이를 참고하여 풀었습니다.
저의 경우 Parametric Search의 알고리즘을 이용하여 풀이하였고 해당 내용은 아래의 글을 참고하였습니다.
파라매트릭 서치(Parametric Search)
목차 1. 파라매트릭 서치(Parametric Search)란? 2. 예시를 통한 파라매트릭 서치(Parametric Search) 3. 시간 복잡도 4. 정리 5. 관련 문제 1. 파라매트릭 서치(Parametric Search)란? Parametric Search에 대해 알아보자.
www.crocus.co.kr
해당 문제에 적용하게 된다면 각 그룹이 갖을 수 있는 합의 최댓값을 결정하는 방식으로 적용하였습니다.
left의 그룹의 합중 가장 작은 값 -> 그룹에 구슬이 1개일 때 최댓값, 즉 제일 큰 구슬
right는 그룹의 합중 가장 큰 값 -> 모든 구슬이 같은 그룹일 경우
mid는 (left + right / 2)을 주어 합이 mid이하가 되도록 그룹을 지어 카운트하게 되면 다음과 같은 경우가 생깁니다.
- mid 이하의 합을 갖는 그룹의 수가 M개 보다 작은 경우
- mid를 낮춰 그룹의 수를 증가 시킨다. -> right = mid - 1;
- mid 이하의 합을 갖는 그룹의 수가 M개 보다 큰 경우
- mid를 높여 그룹의 수를 감소 시킨다. -> left = mid + 1;
주의해야 할 점은 mid 이하의 합을 갖는 그룹의 수가 M개와 같은 경우입니다. 같다고 종료하게되면 mid의 값이 더 낮을 경우도 있기 때문에 주의해야합니다.
코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int N, M;
static int[] beads;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N = Integer.parseInt(st.nextToken()); // 구슬의 수
M = Integer.parseInt(st.nextToken()); // 그룹의 수
beads = new int[N];
int left = 0, right = 0; // left = 그룹의 합중 가장 작은 값 , right = 그룹의 합중 가장 큰 값
st = new StringTokenizer(br.readLine());
for(int i = 0; i < N; i++){
beads[i] = Integer.parseInt(st.nextToken());
left = Math.max(left, beads[i]); // 1개의 구슬이 1개의 그룹일 때 최댓값
right += beads[i]; // 모든 구슬이 같은 그룹인 경우의 합
}
int mid = 0, groupCnt = 0, answer = Integer.MAX_VALUE;
while(left <= right){
mid = (left + right) / 2; // 각 그룹이 갖을 수 있는 합
groupCnt = countGroup(mid); // mid를 이용해 만들 수 있는 그룹의 수
if(M < groupCnt) { // 요구되는 그룹 M 보다 만들 수 있는 그룹의 수가 많은 경우
left = mid + 1; // 각 그룹이 갖을 수 있는 최대합을 높여 그룹의 수 감소
} else { // 요구되는 그룹 M 보다 만들 수 있는 그룹의 수가 적은 경우
right = mid - 1; // 각 그룹이 갖을 수 있는 최대합을 낮춰 그룹의 수 증가
if(mid < answer){ // 그룹의 최솟값 갱신
answer = mid;
}
}
}
StringBuilder sb = new StringBuilder().append(answer).append("\n");
int sum = 0, cnt = 0;
for(int i = 0; i < N; i++){ // 각 그룹별 구슬 갯수 카운트
sum += beads[i];
if(sum <= answer)cnt++; // 그룹합이 최댓값을 넘지 않는다면 count
else if(sum > answer){ // 그룹합이 최댓값을 넘는다면 결과에 구슬수 append
sb.append(cnt).append(" ");
cnt = 1;
sum = beads[i];
M--;
}
if(M == N - i)break; // 남은 그룹의 수와 남은 구슬의 수가 같다면 종료
}
for(int i = 0; i < M; i++){ // 남은 구릅의 수만큼 1로 채우기
sb.append(cnt).append(" ");
cnt = 1;
}
System.out.println(sb.toString());
}
/**
* 각 그룹이 갖을 수 있는 합의 최댓 값 (mid)을 지키며 만들 수 있는 그룹의 수를 카운트
* @param mid
* @return 만들 수 있는 그룹의 수
*/
private static int countGroup(int mid) {
int sum = 0;
int cnt = 0;
for(int i = 0; i < N; i++){
sum += beads[i]; // 그룹 합
if(sum > mid){ // 그룹이 갖을 수 있는 최댓값을 넘는 경우 카운트
sum = beads[i];
cnt++;
}
}
if(sum > 0)cnt++;
return cnt;
}
}'Algorithm > 문제' 카테고리의 다른 글
| [알고리즘] 백준 1062 : 가르침 - JAVA (0) | 2023.09.11 |
|---|---|
| [알고리즘] 백준 14499 : 주사위 굴리기 - JAVA (0) | 2023.09.09 |
| [알고리즘] 백준 12945 : 재미있는 박스 정리 - JAVA (0) | 2023.09.09 |
| [알고리즘] SWEA 11315 : 오목 판정 - JAVA (0) | 2023.07.25 |
| [알고리즘] 백준 1002 : 터렛 - JAVA (0) | 2023.04.20 |
